To bin data or not to bin data ....... that is the question!!
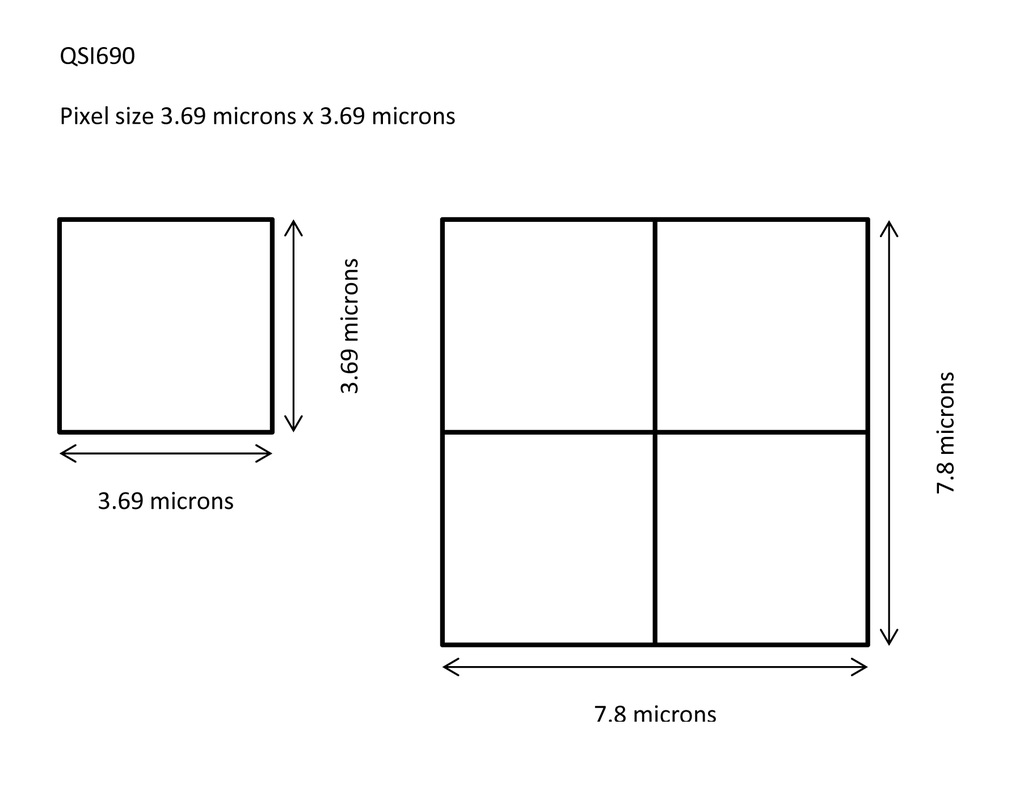
Binning is the process of combining pixels together in the camera to make 'super pixels', which can control the sensitivity and resolution of the camera sensor. In my case, the QSI690, each pixel is 3.69 microns square.
In the diagram below, 1xbin is the diagram on the left. This shows 1 pixel at a square 3.69 micron x 3.69 micron size.
The result of binning 2x2 is the diagram on the right. I now have a 'super pixel' of 7.8 microns x 7.8 microns. This will lead to greater sensitivity (the often quoted sensitivity increase is 4x) which I will also test.
In the diagram below, 1xbin is the diagram on the left. This shows 1 pixel at a square 3.69 micron x 3.69 micron size.
The result of binning 2x2 is the diagram on the right. I now have a 'super pixel' of 7.8 microns x 7.8 microns. This will lead to greater sensitivity (the often quoted sensitivity increase is 4x) which I will also test.
Image resolution or Image scale
This is really important to imagers as we try to make the best of our systems as well as the general sky conditions (seeing). Often referred to as image scale, it is measured in arc seconds per pixel.
It related to two parameters within the imaging system
Irrespective of the image scale your system can achieve, it is limited by two factors working against this figure
Now for the technical part! Nyguist theory suggests that you should be aiming to image at 1/3rd of your seeing, so if your average seeing for example is 3 arc seconds, then you aim to image at 1 arc second.
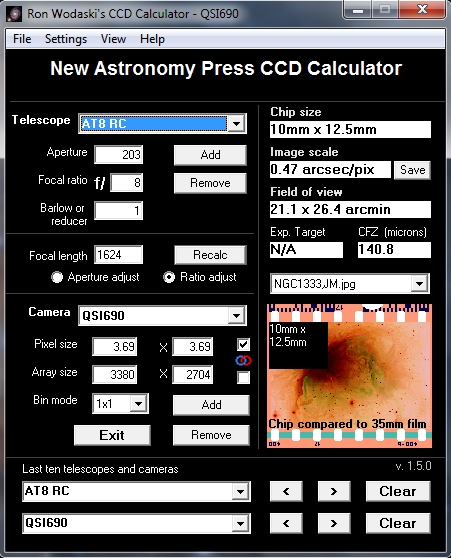
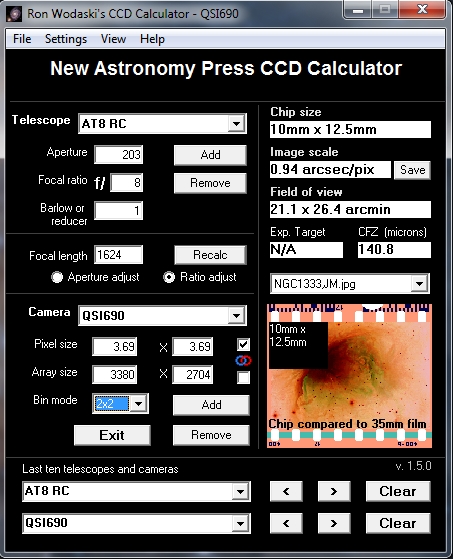
However, I rarely pay much attention to theory and so despite all of this I image generally at 1x bin which gives me an image scale of 0.47. I have recently begun to wonder whether there is an advantage to me using 2x2 bin, which gives me an image scale of 0.94 - As shown below
It related to two parameters within the imaging system
- Pixel size of the camera (in my case 3.69 microns)
- The focal length of the telescope (in my case 1600mm)
Irrespective of the image scale your system can achieve, it is limited by two factors working against this figure
- Seeing - This is described in detail here
- The tracking accuracy of your mount
Now for the technical part! Nyguist theory suggests that you should be aiming to image at 1/3rd of your seeing, so if your average seeing for example is 3 arc seconds, then you aim to image at 1 arc second.
However, I rarely pay much attention to theory and so despite all of this I image generally at 1x bin which gives me an image scale of 0.47. I have recently begun to wonder whether there is an advantage to me using 2x2 bin, which gives me an image scale of 0.94 - As shown below
What does this mean in practice?
I tried to quantify this and recently did some identical exposures, at both 1x1 bin and 2x2 bin, so see if there was a discernible difference to the eye.
Below is a stack of 3x300s in luminance at both 1x1 bin and 2x2 bin. They have been resized so that they are the same and processed in the same way. Can you see a difference? I think that perhaps the 2x2 bin (left hand image) is a little sharper.
Below is a stack of 3x300s in luminance at both 1x1 bin and 2x2 bin. They have been resized so that they are the same and processed in the same way. Can you see a difference? I think that perhaps the 2x2 bin (left hand image) is a little sharper.
From there I decided that it wasn't only about what the eye could see, but two things that I was particularly interested in was whether one image was showing less noise and whether one had smaller stars (lower FWHM).
To look at this I loaded both images into PixInsight where it's able to look at these parameters and plot them for ease.
To look at this I loaded both images into PixInsight where it's able to look at these parameters and plot them for ease.
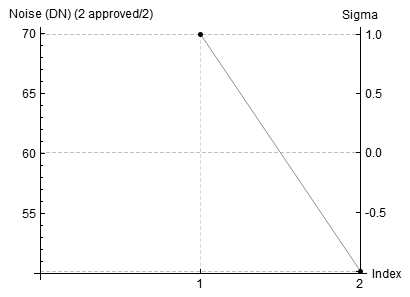
Noise
Firstly the noise plot (In these plots image 1 is 1x1 bin and image 2 is 2x2 bin along the x axis) - Here you can see that there is significantly less noise in the 2x2 bin image, although to my eye it looks to be a larger scale. The noise in the 1x1 bin image looks much finer grained.
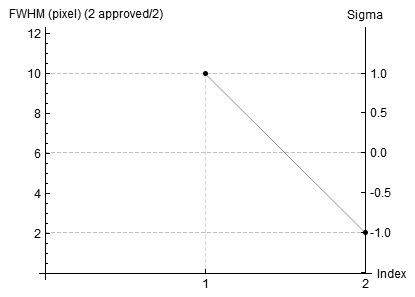
FWHM (size of stars)
This is something important to all imagers. It is generally the way that we prove focus, a smaller FWHM figure and your focus is better. I wondered whether binning images would affect the apparent star size. As you can see here, the overall pixel size throughout the image is significantly smaller with the 2x2 binned images once they have been rescaled to the same size as the 1x1 bin images.
Sensitivity
So far, this looks like being a win win all round. Now lets consider sensitivity, which I mentioned at the start - If you double the pixel size so that your pixels are 2x2, does this lead to an increased sensitivity of 4x as the theory suggests it should?
In order to test this, I took at random 13 identical pixels across both images. I then noted the brightness of these (ADU) which will show an increase in sensitivity.
Here you can see the ADU of each of those randomly selected pixels in both 1x1 bin and 2x2 bin. When averaged out, the difference in my imaging system is 2.93x - That means that my sensitivity is 2.93x greater when 2x2 binned than 1x1 binned.
In order to test this, I took at random 13 identical pixels across both images. I then noted the brightness of these (ADU) which will show an increase in sensitivity.
Here you can see the ADU of each of those randomly selected pixels in both 1x1 bin and 2x2 bin. When averaged out, the difference in my imaging system is 2.93x - That means that my sensitivity is 2.93x greater when 2x2 binned than 1x1 binned.
Conclusion
Based on this analysis, for me the binning argument makes sense. It makes my imaging setup 2.93x more sensitive, so I will collect more faint data. For me this is important. There is a downside of course........ My sensor size of 3380 x 2704 has just halved. But by increasing the resolution of the images in Photoshop to 300DPI, I don't see that as a major problem.
I hope that this has been useful to explain binning and perhaps will give you some thoughts on how you can measure your own increase in sensitivity to get the best out of your imaging time.
I hope that this has been useful to explain binning and perhaps will give you some thoughts on how you can measure your own increase in sensitivity to get the best out of your imaging time.